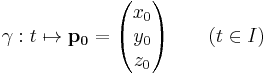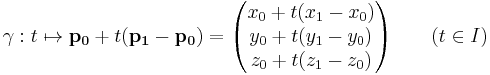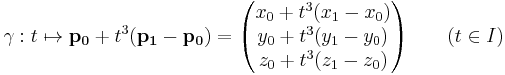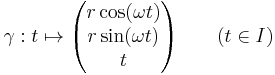Curves in differential geometry

This page addresses the mathematical topic of curves in differential geometry.

Constant curve

Given a point p₀ in R³ and a subinterval I of the real line,

$\mathbf{\gamma}:t \mapsto \mathbf{p_0} = \begin{pmatrix} x_0\\ y_0\\ z_0\\ \end{pmatrix}\qquad (t \in I)$

defines the constant curve, a parametric curve of class C^∞. The image of the constant curve is the single point p. The curve is closed and analytic but not simple.

Line

A slightly more complex example is the line. A parametric definition of a line through the points p₀ and p₁ (p₀ ≠ p₁ and p₀,p₁ ∈ R³) is given by

$\mathbf{\gamma}:t \mapsto \mathbf{p_0} %2B t(\mathbf{p_1} - \mathbf{p_0})= \begin{pmatrix} x_0 %2B t (x_1 - x_0)\\ y_0 %2B t (y_1 - y_0) \\ z_0 %2B t (z_1 - z_0) \\ \end{pmatrix} \qquad (t \in I)$

The image of the curve is a line. Note that

$\mathbf{\gamma}:t \mapsto \mathbf{p_0} %2B t^3 (\mathbf{p_1} - \mathbf{p_0})= \begin{pmatrix} x_0 %2B t^3 (x_1 - x_0)\\ y_0 %2B t^3 (y_1 - y_0) \\ z_0 %2B t^3 (z_1 - z_0) \\ \end{pmatrix} \qquad (t \in I)$

is a different curve but the image of both curves is the same line.

Helix

Given r, ω in R

$\mathbf{\gamma}:t \mapsto \begin{pmatrix} r \cos (\omega t)\\ r \sin (\omega t)\\ t\\ \end{pmatrix}\qquad (t \in I)$

defines a helix circling the z-axis.